Mass-energy and Nuclear Binding Energy

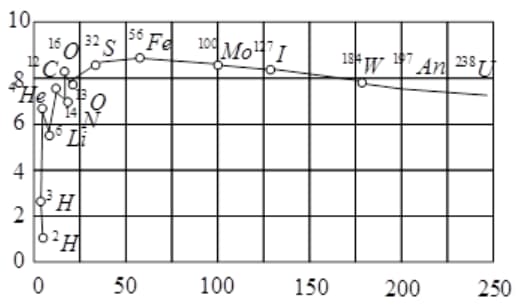
The plot of the binding energy per nucleon versus the mass number A for a large number of nuclei,  $2\le A\le 240$  is shown in Fig. In which range the binding energy per nucleon is constant?

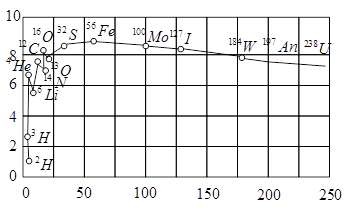
The plot of the binding energy per nucleon versus the mass number A for a large number of nuclei,  $2\le A\le 240$  is shown in Fig. In which range the binding energy per nucleon is constant?

Calculate the energy released in MeV in the following nuclear reaction :<

${}_{92}^{238}\text{U}\to {}_{90}^{234}\text{Th}+{}_2^4\text{He}+\text{Q}$

[Mass of  ${}_{92}^{238}\text{U}$ = 238.05079 u]

Mass of  ${}_{90}^{234}\text{Th}$ = 234.043630 u

Mass of  ${}_2^4\text{He}$  = 4.002600 u

1 u = 931.5 MeV

$\text{Mass of neutron}=1.008665 \mathrm{u}$

The binding energies per nucleon for deuteron (${}_1\mathrm{H}^2$) and helium (${}_2\mathrm{He}^4$) are $1.1 \mathrm{MeV}$ and $7.0 \mathrm{MeV}$ respectively. The energy released when two deuterons fuse to form a helium nucleus (${}_2\mathrm{He}^4$) is

In the nuclear process, ${{}_{6}C}^{11}\to {{}_{5}B}^{11}+{\beta }^{+}+X, X$ stands for _______

The decay of a proton to a neutron is not possible outside a nucleus, because

The nucleus which has the highest binding energy per nucleon is

For a nucleus of mass $M$ having a mass number $A$ and atomic number $Z,$ the expression for mass defect is given by

In the following, column I lists some physical quantities and the column II gives approximate energy values associated with those. Choose appropriate values of energies as per the choices given below

Two protons are separated by $10 \mathrm{\AA }$. Let $F_n$ and $F_e$ be the nuclear force and electrostatic force between them, so

Two deuterons undergo fusion to form a helium nucleus as ${}_1\mathrm{H}^2+{}_1\mathrm{H}^2\to {}_2\mathrm{He}^4+Q$. Given binding energy per nucleon for ${}_1\mathrm{H}^2$ and ${}_2\mathrm{He}^4$ are $1.1 \mathrm{MeV}$ and $7.00 \mathrm{MeV}$, respectively. The $Q$-value is

The voltage applied to an $X$-ray tube is $18 \mathrm{kV}.$ The maximum equivalent mass of photon emitted by the $X$-ray tube will be:

The difference between the mass of a ${}_6{}^{12}\mathrm{C}$ nucleus and the sum of the masses of the individual nucleons is $0.1 \mathrm{u}.$ Which of the following is approximately the binding energy of the nucleus?

A star consist of deuterons. It initially has ${10}^{40}$ deutrons. It produces energy by the processes

${}_{1}H^2+{}_{1}H^2⟶{}_{1}H^3+p$
${}_{1}H^2+{}_{1}H^3⟶{}_{2}H{e}^4+n$
If the average power radiated by the star is $1.6$ $\times {10}^{16}$ watt and masses of nuclei are

$M\left({}_{1}H^2\right)=3AMU, M\left(P\right)\cong M\left(n\right)\cong 1 AMU,$
$M\left({}_{2}H{e}^4\right)=4$$AMU$ and use approximation,
energy equivalent to $1AMU\cong 1000MeV$. Find the time in which the supply of deuteron in the star is exhausted.

A star has a supply of ${10}^{50}$ deuterons. It produces energy via a fusion reaction

${}_1{}^2\mathrm{H}+{}_1{}^2\mathrm{H}⟶{}_1{}^3\mathrm{H}+p$

and ${}_1{}^2\mathrm{H}+{}_1{}^3\mathrm{H}⟶{}_2{}^4\mathrm{He}+n$

where masses of nuclei are

$m\left({}^2\mathrm{H}\right)=2.014 \mathrm{amu}, m\left(p\right)=1.007 \mathrm{amu},$

$m\left(n\right)=1.008 \mathrm{amu}$ and $m\left({}^4\mathrm{He}\right)=4.001 \mathrm{amu}$

If the average power radiated by the star is ${10}^{16} \mathrm{W}$. The deuteron supply of the star is exhausted in a time of the order of $(1 \mathrm{amu}=931 \mathrm{MeV})$

Binding energy of a nucleus is,

The binding energy per nucleon is maximum in the case of,